Do you wanna know everything about Multiple Linear Regression?. If yes, then you are in the right place. Here I will discuss All details related to Multiple Linear Regression. So, give your few minutes to this article in order to get all the details regarding the Multiple Linear Regression.
Hello, & Welcome!
In this blog, I am gonna tell you-
Multiple Linear Regression
When you have more than one Independent variable, this type of Regression is known as Multiple Linear Regression.
Now, you may be wondering What is the Independent variable and What is Regression?.
So, before moving into Multiple Regression, First, you should know about Regression.
What is Regression?
Regression is a supervised machine learning algorithm. It is basically used to predict the target value. The target value is nothing but the Dependent variable.
Let me simplify with the help of an example-
Suppose you have to predict the Property or House Price.
Right?.
So, How you can predict the house Price?.
Definitely with the help of some features of the house.
And these features maybe Age of the House, Number of Bedrooms in the House, or Locality.
So, House Price is dependent on these features. That’s why House price is the Dependent Variable.
And these features Age, Bedroom, and Locality are the Independent Variables.
So, whenever you have such kind of scenario, where you have to predict the value or relationship between variables, You should use Regression.
Regression has various types, but here I will discuss Linear Regression. Because Multiple Linear Regression is a type of Linear Regression.
What is a Linear Regression in Machine Learning?
Linear Regression predicts the continuous dependent variable with the help of independent variables.
In Linear Regression, we have independent variables and one dependent variable.
In Linear Regression, the relationship between a dependent variable and the independent variable is Linear in nature.
Suppose we have one independent variable X and one dependent variable Y. So the relationship between X and Y is Linear. As you can see in this image.
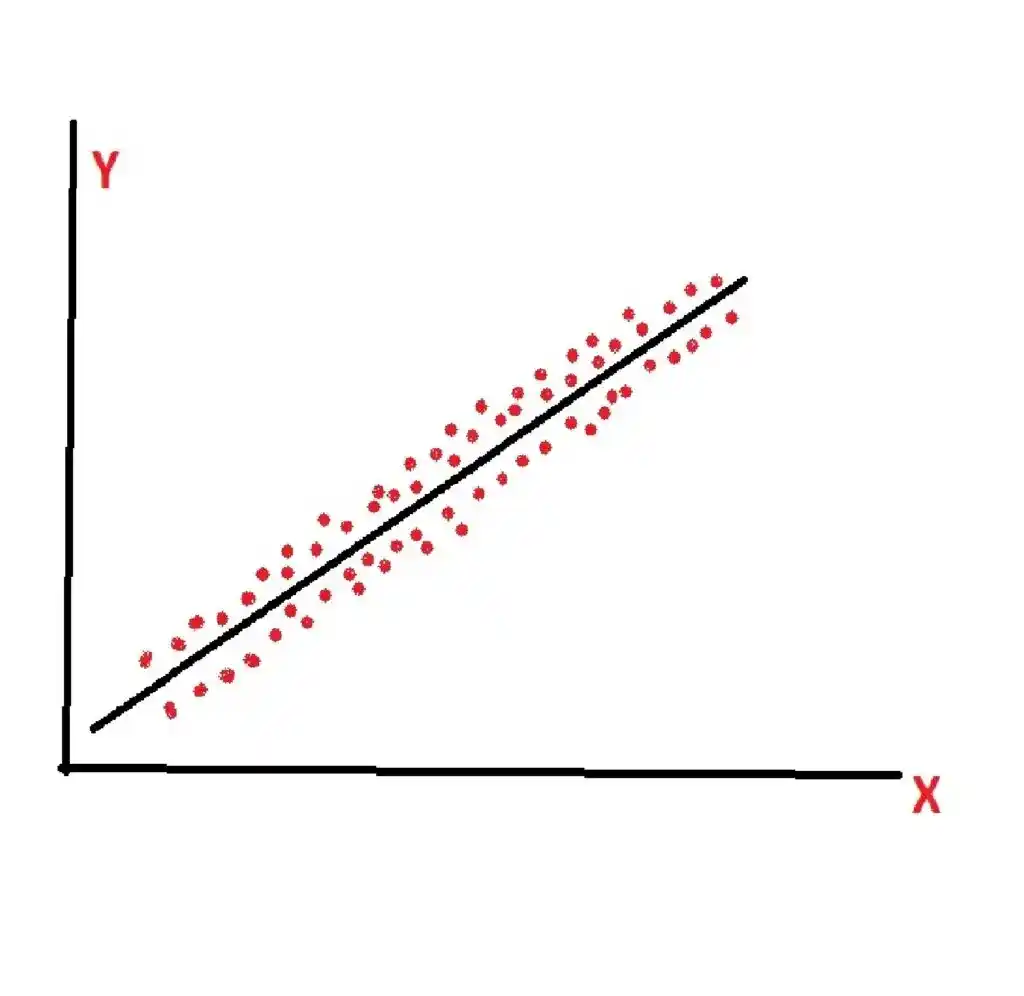
Here the red dots are nothing but data points present in the dataset. This dataset is Linear in nature. That’s why Linear Regression is used here.
So, what does Linear mean here?.
Linear means as the value of X increases, the value of Y also increases.
Linear Regression has two types-
- Simple Linear Regression.
- Multiple Linear Regression.
Here, I will not explain the Simple Regression in detail. If you wanna learn everything about Simple Regression. Then read this article. What Simple Linear Regression is and How It Works?
But in simple words,
When you have only one Independent variable and one dependent variable, so this situation is known as Simple Linear Regression.
The formula for Simple Linear Regression is-
y=b0+b1*x
Where,
y is a Dependent Variable.
x is an independent variable.
b1 is the coefficient for the independent variable x. That represents how a unit change in x affects the unit change in y.
b0 is constant.
I hope now you have a clear idea about Regression, Linear Regression, and Simple Linear Regression.
Right?.
Now, let’s move into Multiple Regression.
Multiple Linear Regression in Machine Learning
When you have multiple or more than one independent variable. Then this scenario is known as Multiple Regression.
Let’s take an example of House Price Prediction.
You can predict the price of a house with more than one independent variable. The age of the house, number of bedrooms, and locality are the independent variables.
The formula of multiple regression is-
y=b0 + b1*x1 + b2*x2 + b3*x3 +…… bn*xn
where,
y is a dependent variable.
x1, x2, x3, ….xn are the independent variables.
b1, b2, b3…bn are coefficients for the independent variables x1, x2, x3, …xn.
b0 is constant.
Here, what are these coefficient, and how to choose coefficient values?
So, let’s see in detail-
What are Coefficients?
Coefficients represent how much the independent variable affects the dependent variable.
Let me simplify it.
The dataset we have may contain various independent variables.
Right?.
Suppose we have a dataset for Student marks prediction. And in that dataset, we have following independent variable or features-
Student’s previous marks, Student Sleep hrs, Student Study hrs, and Student Roll_number.
So, are all these independent variables important for Student marks prediction?
Definitely No.
Why?
Because Student Roll_number doesn’t give any impact on student mark prediction.
Right?
So how do we know which independent variable gives a high impact on the dependent variable and which don’t?
The answer is with the help of coefficients.
Now, you may be wondering how the coefficient helps us to find the impact of each independent variable?
The high the coefficient value of the independent variable, the high impact it has.
Suppose in this Multiple Regression formula, we have four independent variables and their coefficient associated with it.
Student marks= b0 + 3* Student’s previous marks + 2.5* Student Sleep hrs + 4* Student Study hrs + 1* Student Roll_number
Here, “Student Study hrs” has coefficient 4. And that is the highest coefficient value. That’s why “Student Study hrs” give a high impact on Student marks.
Whereas, “Student Roll_number ” has coefficient 1. That means it is not as important for predicting student marks.
So, you can remove this independent variable from your model. Because “Student Roll_number” has a low coefficient and it is not giving too much impact on Student marks or Y.
Now, you understood what is a coefficient and how to know which independent variable gives a high impact.
Right?.
But, now you may be thinking, how to calculate or find the value of coefficients?
So, this happens at the training phase of your model. When you give your dataset to the model, then you see which independent variable is affecting much to the dependent variable. So the independent variable who is giving high impact should have a high coefficient value.
I hope now you understood everything related to the coefficient.
Multiple Regression has some assumptions, so let’s see in the next section.
Assumptions of Multiple Linear Regression
These are the following assumptions-
- Multivariate Normality.
- Independence of Errors.
- Linearity.
- Lack of multicollinearity.
- Homoscedasticity.
So before building a linear regression model, you need to check that these assumptions are true. And then you can proceed to build a Linear Regression Model.
That’s all about assumptions of Multiple Regression.
The next important point is How you deal with categorical variables in Multiple Regression.
Let’s see in the next section-
Dummy Variables in Regression
Suppose we have a dataset for House Price Prediction. Where we have Independent variables- Age of House, Number of Bedrooms, and City where the house is located.
| Age of the House (in Years) | Number of Bedrooms | City | House Price? |
|---|---|---|---|
| 5 | 3 | NewYork | 1000k $ |
| 20 | 2 | California | 700k $ |
| 10 | 4 | California | 850k $ |
| 15 | 3 | NewYork | 900k $ |
Assume, this is our dataset.
So, when we try to write the values into the formula of multiple regression, how we write values for the City variable?
Rest of the variables are numerics, so we can easily write into this formula-
y=b0 + b1*x1 + b2*x2 + b3*x3 +…… bn*xn
But, if we have some categorical variables like City, then What we can do?.
So for that, we need to create a Dummy Variables.
How to create Dummy Variables in Regression?.
First, check how many categories you have. In this example of House Price Prediction, we have two categories- New York, and California.
So for every single category, we need to create a separate column.
| New York | California |
|---|---|
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 1 | 0 |
Here, we created a separate column for each category of City variable.
But, How these 1 and 0 are filled?
You can understand with the help of this image.
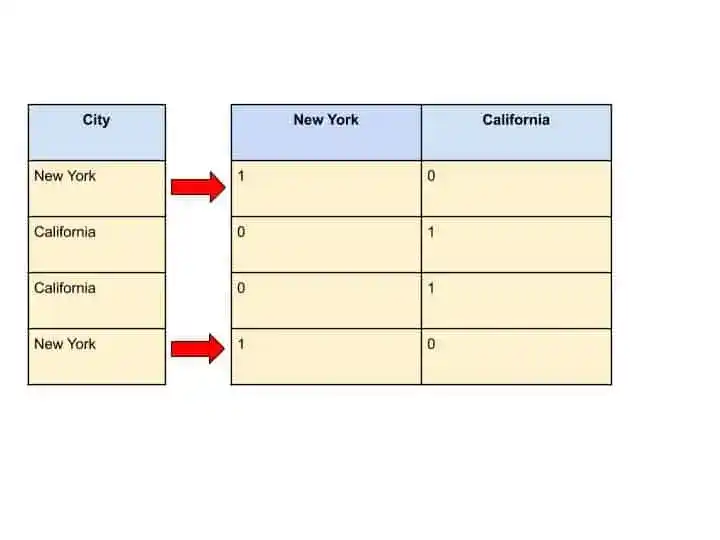
In this image, where New York is present, we filled as 1 and for California, we used 0.
So by doing this approach, we converted it into numeric form. These two new columns are known as Dummy Variables.
Here is one important point, you should know. That you don’t need to use the values of both columns New York and California. You can use only one column value like New York. Because with only the New York column, you are able to know at what place New York is present and at what place California.
Here 1 represents New York and 0 represents California. Therefore, we don’t have to use another column “California”.
In that formula-
y=b0 + b1*x1 + b2*x2 + b3*x3 + b4*D1
Here D1 is the dummy variable of Newyork Column.
So, that’s all about Dummy Variables.
I discussed that all independent variables are not important for prediction. So we can eliminate some unnecessary independent variables with the help of Backward Elimination.
Removing unnecessary independent variables improves the accuracy of the result.
So, let’s see how Backward Elimination eliminates unnecessary independent variables.
Backward Elimination
In backward elimination the first step is-
1. Select a Significance Level in order to stay in the model. Suppose we have chosen a 5% significance level. So, SL= 0.05.
2. Then, build the model with all independent variables present in the dataset.
3. After building the model, check the independent variables with the highest p-value. For more details on the p-value. Read this article.
So, if independent variable has a high p-value than the Significance level (P > SL), remove this independent variable.
4. After removing this independent variable, again build a model from start.
5. Then repeat the same procedure from step 3 until all independent variable has P-value < Significance Level.
By doing these steps, we can remove unnecessary independent variables from our dataset.
Now, its time to wrap up.
Conclusion
In this article, you learned everything related to the Multiple Linear Regression in Machine Learning.
Specifically, you learned-
- What is the Regression, Linear Regression, and Simple Regression?
- What is Multiple Linear Regression, Assumptions, Coefficients, Dummy Variables?
- How to perform Backward Elimination?
I tried to make this article simple and easy for you. But still, if you have any doubt, feel free to ask me in the comment section. I will do my best to clear your doubt.
FAQ
Learn the Basics of Machine Learning Here
Are you ML Beginner and confused, from where to start ML, then read my BLOG – How do I learn Machine Learning?
If you are looking for Machine Learning Algorithms, then read my Blog – Top 5 Machine Learning Algorithm.
If you are wondering about Machine Learning, read this Blog- What is Machine Learning?
Thank YOU!
Though of the Day…
‘ Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young.
– Henry Ford