Do you wanna know about the Multi-Armed Bandit Problem?. If yes, then this blog is just for you. Here I will discuss the Multi-Armed Bandit Problem in a super-easy way. So, give your few minutes to this article in order to get all the details regarding the Multi-Armed Bandit Problem.
Hello, & Welcome!
In this blog, I am gonna tell you-
Multi-Armed Bandit Problem
Multi-Armed Bandit problem is the part of Reinforcement Learning. Therefore before moving into the Multi-Armed Bandit Problem, you should know about Reinforcement Learning.
So, let’s start with Reinforcement Learning.
Reinforcement Learning
Reinforcement Learning is also a machine learning problem. It is based on a self-learning mechanism.
Unlike in supervised learning, where the training dataset is present. But in Reinforcement Learning there is no supervision.
Reinforcement Learning is a hit and trial kind of learning. The main objective of a learner is to get maximum rewards.
The learner interacts dynamically with its environment. And the learner moves from one state to another. These rewards are given based on the action taken by the learner.
The guideline for which action to take in each state is called a Policy.
Therefore, the objective of Reinforcement Learning is to find an optimal policy, so that rewards are maximized.
But there is no supervisor to supervise which action to take. The learner learns from his own experience.
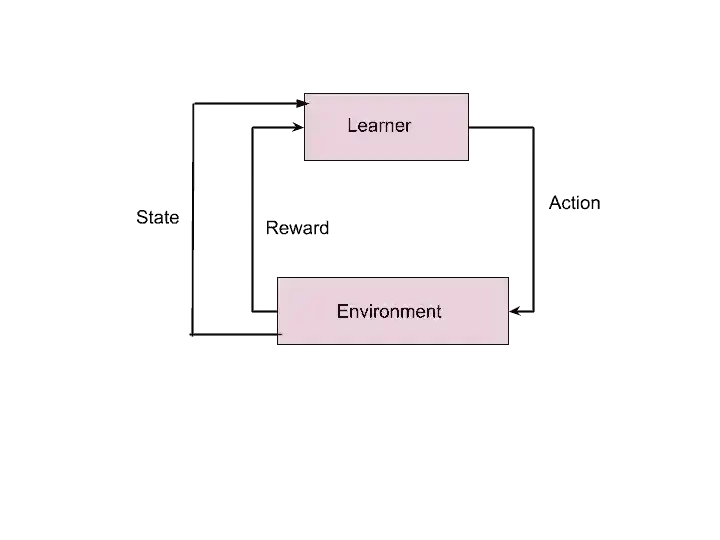
As you see in the image, the learner takes action. And based on the action, the learner gets a reward. This reward may be positive or negative depending upon the action.
So, this way learner learns by itself.
The Multi-Armed Bandit problem is the subset of Reinforcement Learning.
Now, let’s see what is multi-armed bandit problem. It is also known as K-Armed Bandit Problem,
What is K-Armed Bandit Problem
Multi or K-Armed bandit problem is a learner. The learner takes some action and the environment returns some reward value. The learner has to find a policy that leads to maximum rewards.
Before we move into a multi-armed bandit problem, I would like to state a problem. This problem is close to business so that you can better understand.
Suppose, you have to promote some advertisement for any product. And you want to test various types of advertisements for it. Your aim is to select the advertisement that generates more clicks.
Obviously, you don’t know in advance about the number of clicks each advertisement will get. So, you need an algorithm to find the best advertisement.
The traditional approach is A/B Testing. let’s see what is the procedure of A/B Testing.
A/B Testing
In A/B testing, before you start the experiment, you must decide what level of statistical significance is enough.
After that, you start sending visitors to all advertisements simultaneously. And show these ads to visitors randomly. All advertisements get an equal share of visitors.
For example, if you have three types of advertisements for any product. So each advertisement gets one-third of all visitors.
When the level of significance is achieved, you look at which advertisement is the best performer. So you choose the winner advertisement and remove others.
But,
A/B Testing takes long enough time to conduct this experiment. You can’t interrupt it in between experiments. And you can’t change anything. Only you wait patiently.
You are not only waiting for long, moreover, you are also wasting your money. Because you are testing on all advertisements. Most of them are ineffective. But you can’t do anything.
Frustrating Right?
That’s why the Multi-Armed Bandit Problem comes into the scene.
History of Multi-Armed Bandit Problem.
Multi-Armed Bandit Problem was introduced by William R. Thompson in 1933. He wanted to solve the problem of Medical drug experiments. Because it was hard to give ineffective drugs to the patient.
So clinical trials are one of the first intended applications of the K-Armed Bandit Problem.
The name multi-armed bandit itself comes from studies of these two guys. Frederick Mosteller and Robert Bush.
Explore-Exploit Dilemma
Multi or K-Armed Bandit problem work on the explore-exploit scenario.
Explore– An option that looks inferior.
Exploit– Currently the best looking option.
In normal day to life, this scenario exists. Suppose, you like to eat some of your favorite foods daily. So, you feel confident about what you eat. But you are missing the other tasty recipes too, that you don’t know.
And if you try every time new recipes, very likely you will get to eat tasteless food.
In exploitation, you are confident. But in exploration, you take some risk to gather information about the unknown. The one exploration trial might be a failure. But it alarms you to not take this action again.
What is the K-Armed Bandit Problem?
The multi or K-armed bandit problem works on the exploitation-exploration dilemma.
To understand the multi-armed bandit problem, first, see a one-armed bandit problem.
Suppose we have a slot machine, which has one lever and a screen. The screen displays three or more wheels. That looks something like that-
When you pull the lever, the game is activated. This single lever represents the single-arm or one-arm bandit.
So what does a bandit represent here?
The people who play on these machines, they lose more money, than winning. These slot machines have a high probability of taking your money than giving you back. That’s why it is known as Bandit.
So what does Multi-Armed Bandit mean now?
Multi-Armed Bandit is a scenario when you have multiple slot machines. It may be 5, 10, or more.
Let’s assume we have 4 slot machines.
So the question is how you play to maximize your winning on the number of games, you play.
That means if you decide to play 50 times, then how you choose the slot machine out of 4, that maximizes your winnings.
One important thing to consider here is that each machine has a different probability distribution of success.
As a player, you don’t know before the probability distribution of these machines.
Our aim is to find out which slot machines have the best distribution.
Let’s replace these 4 slot machines with their associated distribution.
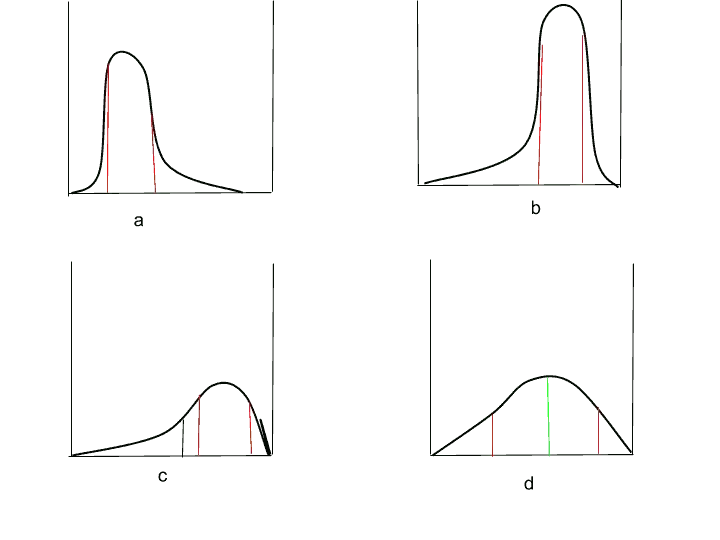
So, do you know, which one is the best distribution among four?.
The answer is the b part distribution. Because it is left-skewed. It has a high mean, median, and mode. But most of the time, we found a different distribution that is similar to the optimal one. And this is not of goal. Our goal is to find the optimal distribution among all slot machines.
So, to find out the optimal distribution, we need to do lots of exploration. And if we don’t do much exploration, then we may settle down with other similar distribution. We think that this is the optimal solution but that is not optimal in reality.
So, to solve this Multi-Armed Bandit problem, there are two algorithms.
- Upper Confidence Bound (UCB).
- Thompson Sampling.
Conclusion
I am not going to discuss these algorithms in this article. Because this article is just to give you a knowledge of the Multi-Armed Bandit Problem.
If you wanna learn, Upper Confidence Bound Algorithm, you can learn from here- Upper Confidence Bound Reinforcement Learning- Super Easy Guide.
I hope, now you understand clearly What is the Multi-Armed Bandit Problem. If you have any doubt, feel free to ask me in the comment section.
Enjoy Machine Learning
All the Best!
Wanna Learn Basics of ML?. Learn Here.
Are you ML Beginner and confused, from where to start ML, then read my BLOG – How do I learn Machine Learning?
If you are looking for Machine Learning Algorithms, then read my Blog – Top 5 Machine Learning Algorithm.
If you are wondering about Machine Learning, read this Blog- What is Machine Learning?
Thank YOU!
Though of the Day…
‘ Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young.
– Henry Ford