Upper Confidence Bound Reinforcement Learning- Super Easy Guide

Do you wanna know about Upper Confidence Bound in Reinforcement Learning?. If yes, then this blog is just for you. Here I will discuss the Upper Confidence Bound in a super-easy way. So, give your few minutes to this article in order to get all the details regarding the Upper Confidence Bound in Reinforcement Learning.

Hello, & Welcome!

In this blog, I am gonna tell you-

Upper Confidence Bound Reinforcement Learning

Before moving into Upper Confidence Bound, you must know a brief about Reinforcement Learning and Multi-Armed Bandit Problem. I have discussed it in my previous article. So if you wanna learn in detail, you can it here- Multi-Armed Bandit Problem- Quick and Super Easy Explanation!.

But, here also I will discuss Reinforcement Learning And Multi-Armed Problem in brief. So that you understand properly Upper Confidence Bound.

So, let’s start with Reinforcement Learning.

Reinforcement Learning

Reinforcement Learning is also a machine learning problem. It is based on a self-learning mechanism.

Unlike in supervised learning, where the training dataset is present. But in Reinforcement Learning there is no supervision.

Reinforcement Learning is a hit and trial kind of learning. The main objective of a learner is to get maximum rewards.

The learner interacts dynamically with its environment. And the learner moves from one state to another. These rewards are given based on the action taken by the learner.

The guideline for which action to take in each state is called a Policy.

Therefore, the objective of Reinforcement Learning is to find an optimal policy, so that rewards are maximized.

So, this way learner learns by itself.

In Reinforcement Learning, we use the Multi-Armed Bandit Problem.

Now, let’s see what is multi-armed bandit problem. It is also known as K-Armed Bandit Problem,

What is Multi-Armed Bandit Problem

Multi-Armed bandit problem is a learner. The learner takes some action and the environment returns some reward value. The learner has to find a policy that leads to maximum rewards.

To understand the multi-armed bandit problem, first, see a one-armed bandit problem.

Suppose we have a slot machine, which has one lever and a screen. The screen displays three or more wheels. That looks something like that-

When you pull the lever, the game is activated. This single lever represents the single-arm or one-arm bandit.

So what does a bandit represent here?

The people who play on these machines, they lose more money, than winning. These slot machines have a high probability of taking your money than giving you back. That’s why it is known as Bandit.

So what does Multi-Armed Bandit mean now?

Multi-Armed Bandit is a scenario when you have multiple slot machines. It may be 5, 10, or more.

Let’s assume we have 4 slot machines.

So the question is how you play to maximize your winning on the number of games, you play.

That means if you decide to play 50 times, then how you choose the slot machine out of 4, that maximizes your winnings.

One important thing to consider here is that each machine has a different probability distribution of success.

So, do you know, which one is the best distribution among four?.

So, to find out the optimal distribution, we need to do lots of exploration. And if we don’t do much exploration, then we may settle down with other similar distribution. We think that this is the optimal solution but that is not optimal in reality.

One more example of the Multi-Armed Bandit Problem is Advertisement.

Suppose The advertiser has to find out the click rate of each ad for the same product. The objective of the advertiser is to find the best advertisement. So, these are the steps of Multi-Armed Bandit Problem–

1. We have m ads. The advertiser displays these ads to there user when the user visits the web page.
2. Each time a user visits the web page, that makes one round.
3. At each round, the advertiser chooses one ad to display to the user.
4. At each round n, ad j gets reward rj(n) ∈ {0,1} : rj(n)=1 if user clicked on the ad, and 0 if user didn’t click the ad.
5. The advertiser’s goal is to maximize the total reward from all rounds.

So, to solve this Multi-Armed Bandit problem, the Upper Confidence Bound algorithm is used.

Let’s move into Upper Confident Bound, and see some cool stuff. 😎

Upper Confidence Bound Algorithm.

Here, I am gonna tell you the whole working of Upper Confidence Bound. That means What happens in the background of this algorithm. It’s not gonna complicated. It’s fun.

So Are you Excited?

Yes, let’s start. 👍

Suppose, these are the four ads, we have. And we have to find the optimal one or who has more click rate.

Each ad has a distribution behind it. And by looking at them, we can’t tell which one is best. Right?

But, after performing Upper Confidence Bound, we will find the best one.

Suppose, these are the distribution behind every advertisement.

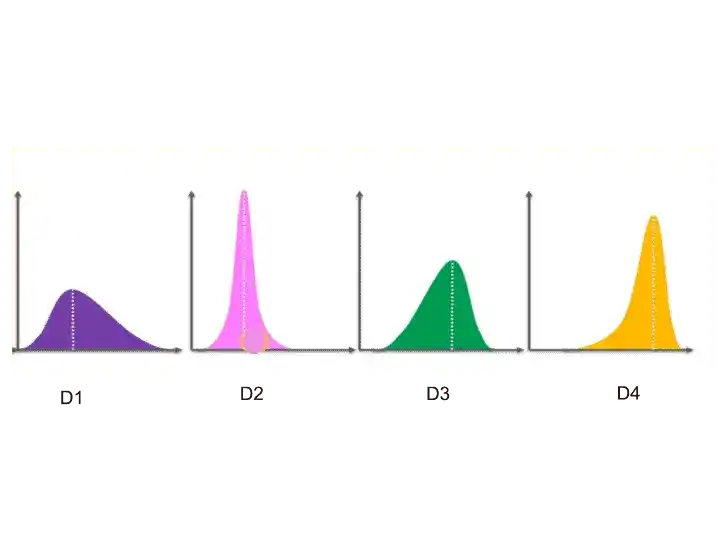
So, by looking at this distribution, you can tell which one is the best ad.

The D4 distribution is the left-skewed and that’s why Ad 4 is the best.

But,

We don’t know it before. This is not defined in our problem. Upper Confident Bound Algorithm will find out. I used this visualization just for your better understanding.

We have to find out with the help of Upper Confidence Bound.

How does Upper Confidence Bound Algorithm work?

Step 1-

So, to understand how Upper confidence bound work, let’s transform these vertical lines of distribution into the horizontal line. Something Like that-

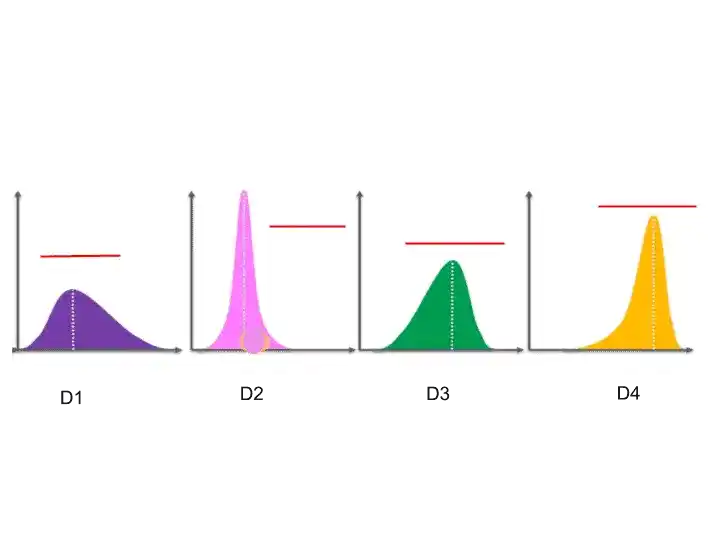
So, after transforming into horizontal lines, it will look something like that-

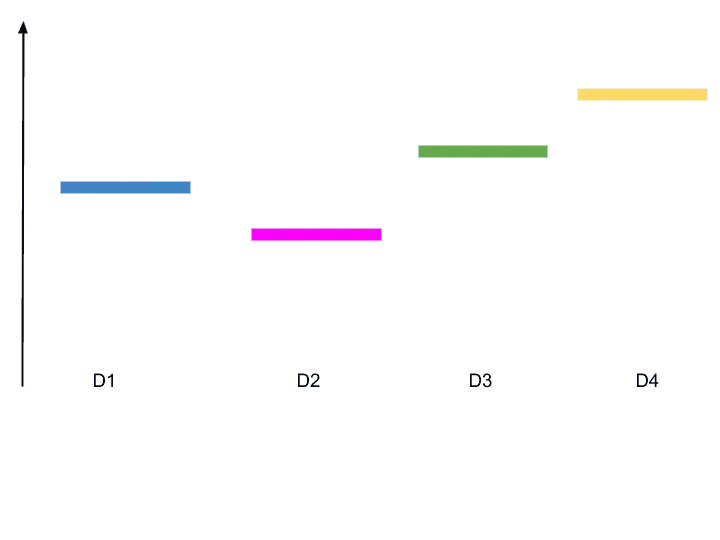
So, these are the expected values or return for each of these distributions for each ad.

Step 2-

The upper confidence bound assumes some starting point for each distribution. As we don’t know which ad is best, so all ads have the same starting point.

So, suppose each ad has this starting point, as shown in the image.

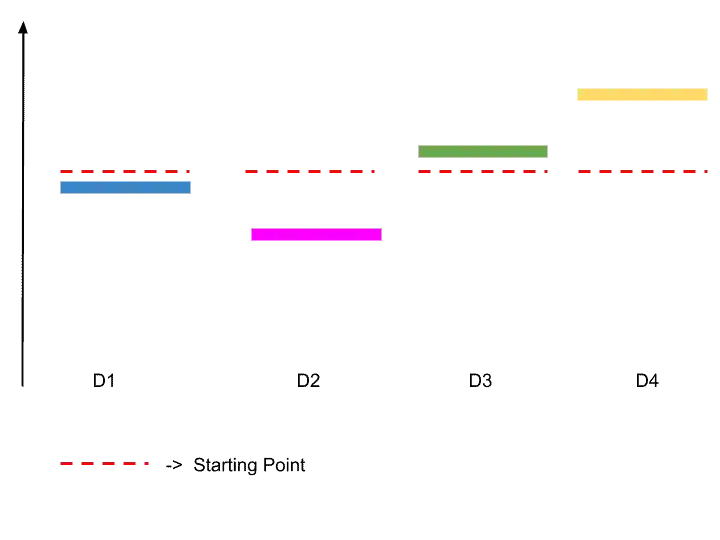
Step 3-

Now, the formula behind this upper confidence bound algorithm creates confidence bound. And these bounds are designed in such a way that we have a very high level of certainty that confidence bound will include the actual expected return.

So the confidence bound looks something like that.

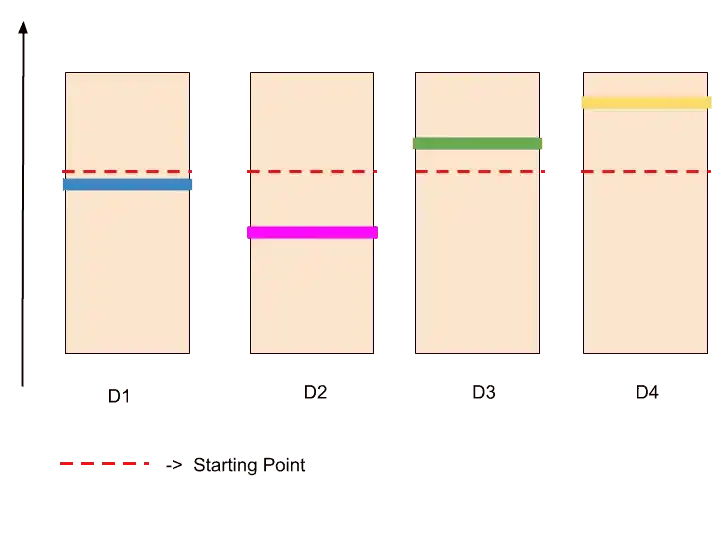
Step 4-

As Upper confidence bound work on upper bound, so we will consider those distributions who are closer to the upper bound.

But, as of now, all have on the same level.

That’s why suppose we have chosen randomly one ad D2.

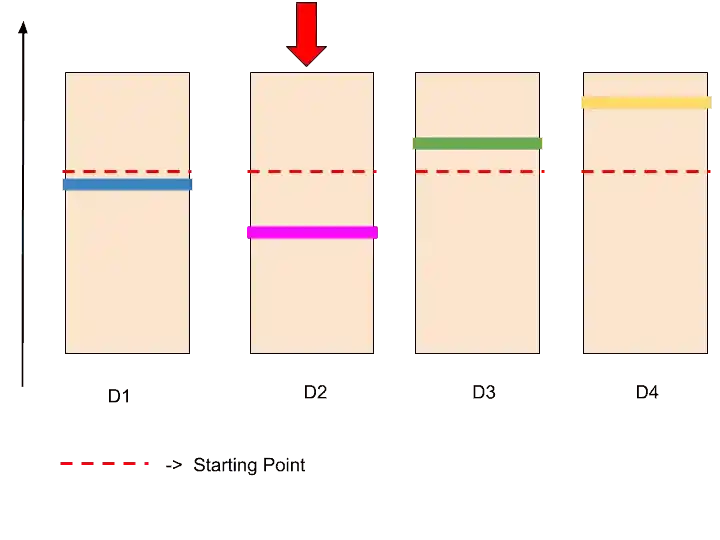
Step 5-

So we are testing that if we display this ad to the user, so what is the response. Assume that the user didn’t click on this ad.

Because the user didn’t click on this ad, so the confidence bound becomes lower. And the red dotted line ( the starting point) also goes down. The confidence bound shrink also, which means it becomes smaller.

So now, it looks something like that.

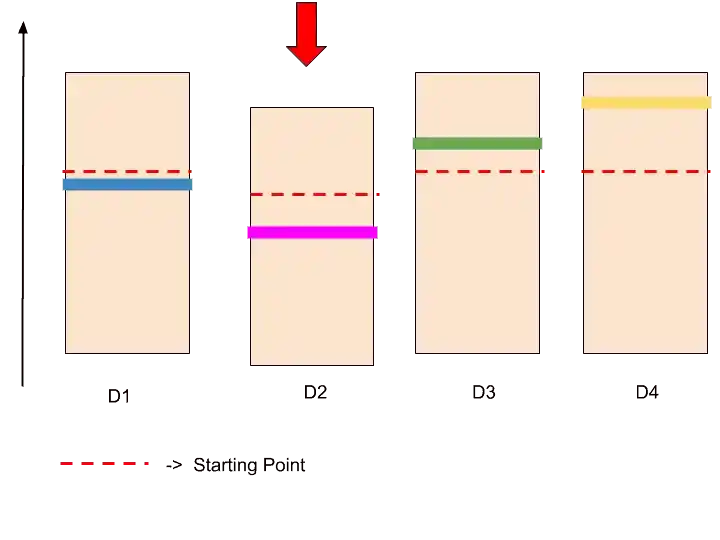
Every time, the confidence bound may go up or low, depending upon the ad is clicked or not. Along with that, the size of confidence bound also becoming smaller. Confidence Bound is the square boundary.

And the Upper Confidence Bound means the upper boundary of this square.

I hope now it clear to you. Right?. 👍

Step 6-

So, the next step is to find the next ad with the high confidence bound. It may D1, D3, and D4. Because of they all on the same level.

Assume, we have chosen randomly this ad D3.

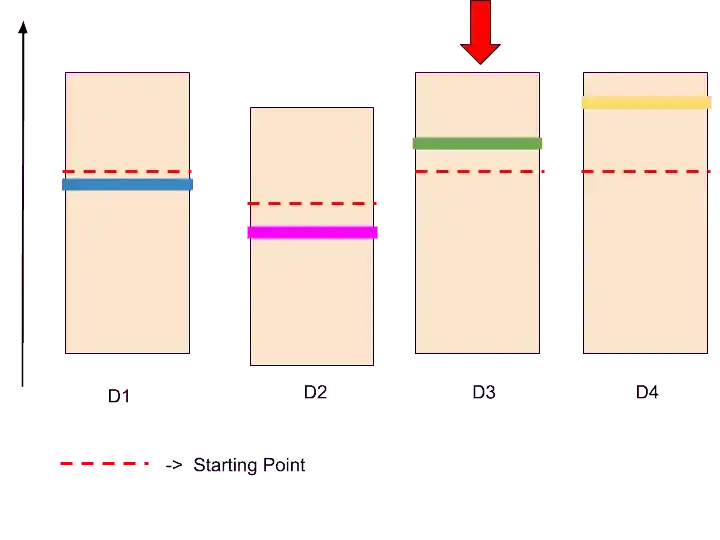
We perform the same task as we did with D2. So, again we display this ad to the user. The user will either click it or not.

Let’s assume users click on the ad. So this ad or distribution goes a little bit up.

After this step, it looks like that.

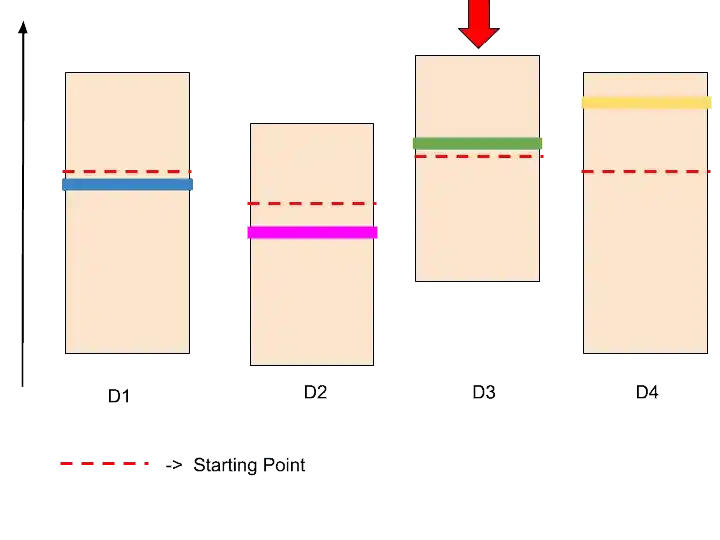
As you can see in the image, D3 goes up from other distribution. So this D3 has reached the upper confidence level. And this is the end. We found the best ad.

But……

This is not the end.

Because in the upper confidence bound algorithm, the size of confidence bound also becoming smaller. Therefore, the confidence bound of D3 shrinks.

After shrinking, it looks something like that.

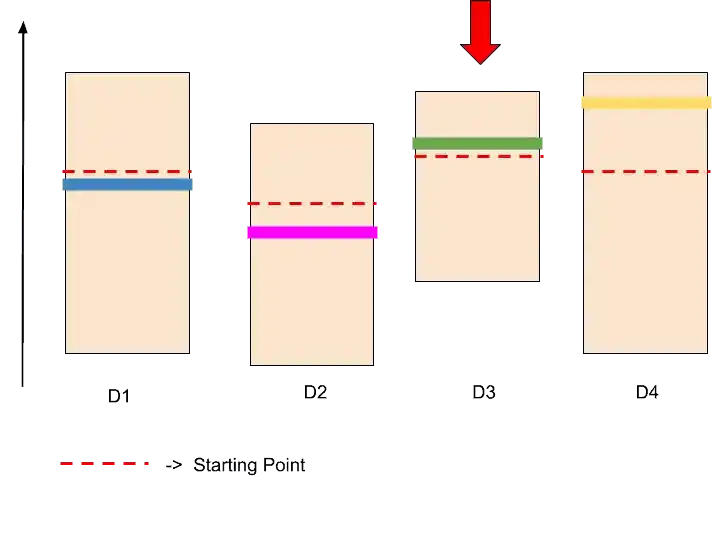
In that image, you can see that the red dotted line goes up, but the size of confidence bound becomes small.

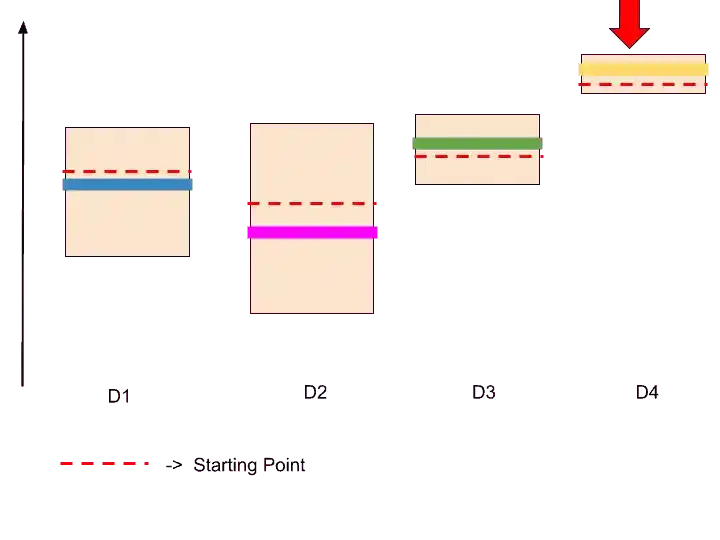
Now, D3 is not on the top of other ads.

Step- 7

So, now we are going to look for the next highest confidence bound. It may be D1 or D4. Because both are on the same level.

So this process continues until we find the best ad. There may be hundreds or thousands of iterations.

The best ad is defined who has highest confidence bound.

After so many iterations, we found that D4 has the highest confidence bound. Therefore, Ad 4 is the best ad that has more click rates than others.

So, that’s the whole concept behind the upper confidence bound algorithm. And that’s how it solves the Multi-Armed Bandit problem.

Conclusion

The upper confidence Bound algorithm saves your time. As in A/B Testing, it takes more time and money. The upper confidence Bound Algorithms works perfectly for Advertisement or for any Campaigns.

I hope you enjoyed while reading this article. And you understand properly how Upper Confidence Bound Algorithms Works.

If you have any doubt, feel free to ask me in the comment section.

Enjoy Machine Learning

All the Best!

Wanna Learn Basics of ML?. Learn Here.

Are you ML Beginner and confused, from where to start ML, then read my BLOG – How do I learn Machine Learning?

If you are looking for Machine Learning Algorithms, then read my Blog – Top 5 Machine Learning Algorithm.

If you are wondering about Machine Learning, read this Blog- What is Machine Learning?

Thank YOU!

Though of the Day…

‘ Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young.

– Henry Ford